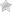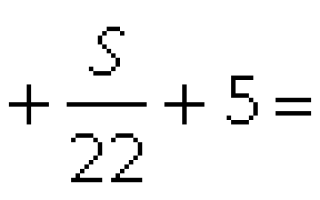Со скоростью 240 км/ч в воздухе встретились две дорогие иномарки

26583. Два велосипедиста одновременно отправились в 240-километровый пробег. Первый ехал со скоростью, на 1 км/ч большей, чем скорость второго, и прибыл к финишу на 1 час раньше второго. Найти скорость велосипедиста, пришедшего к финишу первым. Ответ дайте в км/ч.

Примем скорость  второго велосипедиста за х (км/ч). Тогда  скорость первого  равна х+1 (км/ч). Расстояние оба проехали  одинаковое — 240 километров.  Осталось записать время.

• Формула времени имеет вид:
• Значит первый затратит на дорогу
• Второй
• Таблица:
• Сказано, что первый прибыл на час раньше, то есть он затратил время на движение и ещё час ожидал пока прибудет второй. Значит время, затраченное первым на передвижение плюс час ожидания второго, равно времени нахождения в пути второго:
• Можно сказать по-другому: выражение  «первый прибыл на час раньше», означает, что он затратил на пробег на час меньше, чем второй, то есть:
• Умножаем левую и правую части на х(х+1):
• Получили, что скорость второго велосипедиста равна 15 км/ч.
• Значит скорость первого равна 15 + 1 = 16 км/ч.
• Отрицательный ответ не является решением, так скорость не может быть величиной отрицательной.
• Ответ: 16

Категория: Движение | Задания 11

Подготовка к ОГЭ по математике. Полный курс!

Онлайн подготовка по математике. Годовой курс!

Подготовка к ЕГЭ – ИСТОРИЯ и ОБЩЕСТВОЗНАНИЕ!

*Нажимая на кнопку, я даю согласие на рассылку, обработку персональных данных и принимаю политику конфиденциальности.

Источник: http://matematikaege.ru/dvihzenie/26583-dva-velosipedista-odnovremenno.html

Математика: Задачи на движение

Этот раздел посвящен текстовым задачам на движение.

В них допускается определенная идеализация: считается, что тела движутся прямолинейно и равномерно, скорости постоянны в течение определенных промежутков времени, не меняются при поворотах и т. д.

, движущиеся тела считаются материальными точками (если не оговорено противное), т.е. не имеющими размеров и массы (вернее, их размеры и масса несущественны для решения задачи).Основные типы задач на движение:

1) задачи на движение по прямой (навстречу и вдогонку),2) задачи на движение по замкнутой трассе,3) задачи на движение по воде,4) задачи на среднюю скорость,5) задачи на движение протяженных тел.

Рассмотрим более подробно каждый из этих типов задач, выделив, где необходимо, базовые задачи.Движение навстречуОдним из методов решения задач является создание упрощенной модели.Пример 1.Рассмотрим два объекта, движущихся навстречу с указанными на рисунке скоростями.Пусть прошла 1 минута. Как изменилось положение объектов:Видим, что расстояние между объектами сократилось на 15 + 10 = 25 метров. Таким образом, объекты сближаются со скоростью, равной сумме их скоростей. Значит, время их встречи равно t = 100/(15 + 10) = 4 (мин).Если расстояние между двумя телами равно s, а их скорости v1 и v2, то время t, через которое они встретятся, находится по формулеt = S/(v1 + v2 ).Пример 2.Расстояние между городами А и В равно 435 км. Из города А в город В со скоростью 60 км/ч выехал первый автомобиль, а через час после этого навстречу ему из города В выехал со скоростью 65 км/ч второй автомобиль. На каком расстоянии от города А автомобили встретятся? Ответ дайте в километрах.Решение.Через час после выезда первого автомобиля расстояние между автомобилями стало равно 435 – 60 = 375 (км), поэтому автомобили встретятся через времяt = 375/(60 + 65) = 3 (ч)Таким образом, до момента встречи первый автомобиль будет находиться в пути 4 часа и проедет 60 · 4 = 240 (км).Ответ: 240.Движение вдогонкуПример 3.Рассмотрим два объекта, один из которых догоняет другой, с указанными на рисунке скоростями.Пусть прошла 1 минута. Как изменилось положение объектов:Видим, что расстояние между объектами сократилось на 15 – 10 = 5 метров. Т.е. объекты сближаются со скоростью, равной разности их скоростей. Значит, время, за которое первый объект догонит другой, или время их встречи равноt = 100/(15 – 10) = 20 (мин).Если расстояние между двумя телами равно s, и они движутся по прямой в одну сторону со скоростями v1 и v2 соответственно (v1 > v2) так, что первое тело следует за вторым, то время t, через которое первое тело догонит второе, находится по формуле t = S/(v1 – v2 ).Пример 4.Два пешехода отправляются в одном направлении одновременно из одного и того же места на прогулку по аллее парка. Скорость первого на 1,5 км/ч больше скорости второго. Через сколько минут расстояние между пешеходами станет равным 300 метрам?Решение.Время t в часах, за которое расстояние между пешеходами станет равным 300 метрам, т. е. 0,3 км, находим по формулеt = 0,3/(v + 1,5 – v) = 0,3/1,5 = 0,2 (ч)Следовательно, это время составляет 12 минут.Ответ: 12.Движение по окружности (замкнутой трассе)Пример 5.Рассмотрим движение двух точек по окружности длины L в одном направлении при одновременном старте со скоростями v1 и v2 (v1 > v2) и ответим на вопрос: через какое время первая точка будет опережать вторую ровно на один круг? Считая, что вторая точка покоится, а первая приближается к ней со скоростью v1 – v2, получим, что условие задачи будет выполнено, когда первая точка поравняется в первый раз со второй. При этом первая точка пройдет расстояние, равное длине одного круга, и искомая формула ничем не отличается от формулы, полученной для задачи на движение вдогонку: t = L/(v1- v2) .Итак, если две точки начинают движение по окружности в одну сторону со скоростями v1 и v2 соответственно (v1 > v2), то первая точка приближается ко второй со скоростью v1 – v2 и в момент, когда первая точка в первый раз догоняет вторую, она проходит расстояние на один круг больше.Пример 6.Из одной точки круговой трассы, длина которой равна 14 км, одновременно в одном направлении стартовали два автомобиля. Скорость первого автомобиля равна 80 км/ч, и через 40 минут после старта он опережал второй автомобиль на один круг. Найдите скорость второго автомобиля. Ответ дайте в км/ч.Решение.Пусть скорость второго автомобиля х км/ч. Поскольку 40 минут составляют 2/3 часа и это — то время, за которое первый автомобиль будет опережать второй на один круг, составим по условию задачи уравнение14/(80-x) = 2/3, 160 – 2x = 42, т.е. х = 59 (км/ч).Ответ: 59.Движение по водеВ задачах на движение по воде скорость течения считается неизменной. При движении по течению скорость течения прибавляется к скорости плывущего тела, при движении против течения — вычитается из скорости тела. Скорость плота считается равной скорости течения.Пример 7.Теплоход, скорость которого в неподвижной воде равна 25 км/ч, проходит по течению реки и после стоянки возвращается в исходный пункт. Скорость течения равна 3 км/ч, стоянка длится 5 часов, а в исходный пункт теплоход возвращается через 30 часов после отплытия из него. Сколько километров прошел теплоход за весь рейс?Решение.Пусть искомая величина равна 2S.

S (км)	v (км/ч)	t (ч)
По течению	S	25 + 3 = 28	S/28
Против течения	S	25 – 3 = 22	S/22
Стоянка	–	–	5

Составим по условию задачи уравнение ,откуда .Значит, искомое расстояние равно 616 км.Ответ: 616.Средняя скоростьНапомним, что средняя скорость вычисляется по формулегде S — путь, пройденный телом, a t — время, за которое этот путь пройден. Если путь состоит из нескольких участков, то следует вычислить всю длину пути и всё время движения. Например, если путь состоял из двух участков протяженностью S1 и S2, скорости на которых были равны соответственно v1 и v2, то где Пример 8.Первую треть трассы велосипедист ехал со скоростью 12 км/ч, вторую треть — со скоростью 16 км/ч, а последнюю треть — со скоростью 24 км/ч. Найдите среднюю скорость велосипедиста на протяжении всего пути. Ответ дайте в км/ч.Решение.Обозначим длину всей трассы через 3S. Тогда первую треть трассы велосипедист проехал за время t1 = S/12, вторую треть — за время t2 = S/16, последнюю треть — за время t3 = S/24. Значит, время, потраченное им на весь путь, равно t1 + t2 + t3,т. е. Поэтому искомая средняя скорость находится по формулеОтвет: 16.Движение протяженных тел

В задачах на движение протяжных тел требуется определить длину одного из них. Наиболее типичные ситуации: определение длины поезда проезжающего мимо

• придорожного столба
• идущего параллельно путям пешехода
• лесополосы определенной длины
• другого двигающегося поезда

Если поезд движется мимо столба (светофора, человека), то он проходит расстояние S равное его длине L:S = L = vt.Если поезд движется мимо протяженной лесополосы, то он проходит расстояние равное сумме длины самого поезда L1 и лесополосы L2 :S = L1 + L2.Пример 9.Поезд, двигаясь равномерно со скоростью 60 км/ч, проезжает мимо придорожного столба за 30 секунд. Найти длину поезда в метрах.Решение.Зная скорость движения v = 60 км/ч = 1000 м/мин и время, за которое он проезжает мимо столба t = 30 сек. = 1/2 мин, можно найти длину поезда как пройденное расстояние S = vt = 1000·1/2 = 500 (м).Ответ: 500.Пример 10.Поезд, двигаясь равномерно со скоростью 90 км/ч, за 1 минуту проезжает мимо лесополосы, длина которой 800 м. Найти длину поезда в метрах.Решение.Зная скорость движения v = 90 км/ч = 1500 м/мин и время, за которое он проезжает мимо лесополосы длиной 800 метров за t = 1 мин, можно найти длину поезда как пройденное расстояние S = vt = 1500·1 = 1500 м минус длина лесополосы 800 метров и получим длину поезда равную 700 метров.Ответ: 700.Пример 11.Поезд проходит мост длиной 450 м за 45 с, а мимо будки стрелочника — за 15 с. Найти длину поезда и его скорость.Решение.Пусть скорость поезда v м/с. Тогда длина поезда L = 15v (м). За 45 с поезд проходит расстояние 45v (м) или (450 + 15v) м. Получаем уравнение:45v = 450 + 15v, откуда v = 15, L = 15v = 225.Ответ: длина поезда 225 м, а его скорость 15 м/с.Пример 12.По морю параллельными курсами в одном направлении следуют два сухогруза: первый длиной 120 метров, второй — длиной 80 метров. Сначала второй сухогруз отстает от первого и в некоторый момент времени расстояние от кормы первого сухогруза до носа второго сухогруза составляет 400 метров. Через 12 минут после этого уже первый сухогруз отстает второго так, что расстояние от кормы второго сухогруза до носа первого равно 600 метрам. На сколько километров в час скорость первого сухогруза меньше скорости второго?Решение.Через 12 минут:Будем считать, что первый сухогруз неподвижен, а второй приближается к нему со скоростью х (м/мин), равной разности скоростей второго и первого сухогрузов. Тогда за 12 минут второй сухогруз проходит расстояние L = 400 + 120 + 80 + 600 = 1200 (м).Поэтому х = 1200/12 = 100 (м/мин) = 6 (км/ч).Ответ: 6.Задачи для тренировкиУсловие задач часто для удобства представляют либо в виде рисунка, либо в виде таблицы, либо в виде того и другого.Пример 13.Расстояние между двумя городами скорый поезд проходит на 4 часа быстрее товарного и на 1 час быстрее пассажирского. Найти скорости товарного и скорого поездов, если известно, что скорость товарного поезда составляет 5/8 от скорости пассажирского и на 50 км/ч меньше скорости скорого.Решение.Пусть v км/ч — скорость товарного поезда (v > 0), t ч — время движения скорого поезда (t > 0). Составим таблицу.

Расстояние (км)	Скорость (км/ч)	Время (ч)
Скорый поезд	(v+50)t	v+50	t
Пассажирский поезд	8/5 v(t+1)	8/5 v	t+1
Товарный поезд	v(t+4)	v	t+4

По условию задачи поезда прошли одно и то же расстояние. Получаем цепочку (систему) уравнений (v + 50)t = 8/5 v(t + 1) = v(t + 4).vt + 50t = vt + 4v 50t = 4v v = 12,5t,1,6vt + 1,6v = vt + 4v 0,6vt = 2,4v |: v > 0 t = 4, v = 12,5 · 4 = 50.50 км/ч — скорость товарного поезда.50 + 50 = 100 (км/ч) — скорость скорого поезда.Ответ: 50, 100.Пример 14.Два туриста вышли одновременно навстречу друг другу из пунктов А и В. Каждый шел с постоянной скоростью и, придя, в конечный пункт, немедленно поворачивал обратно. Первый раз они встретились в 12 км от пункта В, второй раз — в 6 км от А через 6 часов после первой встречи. Найти расстояние между пунктами и скорости туристов.Решение.Используя схему движения туристов, составим таблицу.

Туристы/Путь	S	v	t
I	АС	6 + S
СВ	12
ВД	12 + S
II	ВС	12
СА	6 + S
АД	6

Из корней последнего уравнения (-1 и 4) только v2 = 4 (км/ч) походит по смыслу. Тогда v1 = v2 + 2 = 4 + 2 = 6 (км/ч).S = 6v2 – 12 = 24 – 12 = 12 (км).Весь путь 18 + S = 18 + 12 = 30 (км).Ответ: 30, 4, 6.В следующей задаче встречается два типа задач: «движение навстречу» и «обычное движение».Пример 15.Два велосипедиста выехали одновременно из пунктов А и В навстречу друг другу. Велосипедист, ехавший из А, прибыл в В через 4 часа после встречи, а велосипедист, ехавший из В, прибыл в А через 9 часов после встречи. Сколько часов был в пути каждый велосипедист?Решение.Пусть весь путь от А до В равен S км, v1 и v2 — скорости велосипедистов и tв — время, прошедшее с момента начала движения до встречи велосипедистов.

S	v	t
I  до встречи
II  до встречи
I после встречи	4
II после встречи	9

Первый и второй велосипедисты после встречи проехали весь путь S, который найдем из выражений для S1 и S – S1 :S = S1 + (S – S1 ) = 4v1 + 9v2, тогда выражение для tв : tв = (4v1 + 9v2)/( v1 + v2). Имеем систему уравнений:Тогда Тогда значения времени, о которых спрашивается в задаче: tв + 4 = 10 ч, tв + 9 = 15 ч.Ответ: 10, 15. Видеолекция «Задачи на движение»:

Перейти к выполнению теста: Тест. Задачи на движение

Источник: http://free.megacampus.ru/xbookM0005/book/part-026/page.htm

Задания №11. Задачи на движение по прямой

Елена Репина 2013-10-30 2015-09-04

Задачи на движение по прямой

• На этот раз рассматриваем задачи из открытого банка заданий ЕГЭ по математике на прямолинейное движение.
• Смотрите также другие типы Задач №11 ЕГЭ по математике:
  1 (на среднюю скорость), 2 (на движение по окружности), 3 (движение по воде), 4 (на работу), 6 (на прогрессии), 7 (на смеси и сплавы).
• Также смотрите видеолекцию «Текстовые задачи» здесь.

Задачи В14 могут встретиться на ЕГЭ по математике совсем простые, где может даже не потребоваться введение переменной. Чаще будут встречаться задачи, сводимые к решению квадратных уравнений (кстати, что делать, если дискриминант намечается слишком большой, – смотрите здесь и здесь).

Задание 1

Два велосипедиста одновременно отправились в 130-километровый пробег. Первый ехал со скоростью, на 3 км/ч большей, чем скорость второго, и прибыл к финишу на 3 часа раньше второго. Найти скорость велосипедиста, пришедшего к финишу первым. Ответ дайте в км/ч.

Решение:

+ показать

Пусть км/ч – скорость второго велосипедиста. Тогда согласно условию км/ч – скорость первого велосипедиста.

1. Оба велосипедиста проехали 130 км.
2. Третью колонку таблицы заполняем автоматически, пользуясь формулой :
4. Время движения первого велосипедиста меньше, чем время движения второго на 3 часа, поэтому

• Откуда   км/ч.
• К финишу придет первым велосипедист со скоростью , поэтому в ответ отправляем величину (км/ч).
• Ответ: 13.

Задание 2

Из пункта А в пункт В, расстояние между которыми 60 км, одновременно выехали автомобилист и велосипедист. Известно, что в час автомобилист проезжает на 110 км больше, чем велосипедист. Определите скорость велосипедиста, если известно, что он прибыл в пункт В на 5,5 часов позже автомобилиста. Ответ дайте в км/ч.

1.  Решение:
2. + показать
3. Задача очень похожа на предыдущую.
4. Если не  знаете как извлечь корень из большого дискриминанта, загляните сюда и сюда.
5. Откуда км/ч.
6. Ответ: 10.

Задание 3

Велосипедист выехал с постоянной скоростью из города А в город В, расстояние между которыми равно 80 км. На следующий день он отправился обратно со скоростью на 2 км/ч больше прежней. По дороге он сделал остановку на 2 часа. В результате он затратил на обратный путь столько же времени, сколько на путь из А в В. Найдите скорость велосипедиста на пути из А в В. Ответ дайте в км/ч.

Решение:

+ показать

Пусть км/ч – скорость велосипедиста на пути АВ. Тогда согласно условию км/ч – скорость велосипедиста на пути ВА.

• Длину пути АВ (ВА) 80 км.
• Третью колонку таблицы заполняем автоматически, пользуясь формулой :
• Время движения велосипедиста  на пути ВА меньше, чем время движения  на пути АВ на  2 часа, поэтому
• Откуда вытекает, что (км/ч).
• Ответ: 8.

Задание 4

Из пункта A в пункт B одновременно выехали два автомобиля. Первый проехал с постоянной скоростью весь путь.

Второй проехал первую половину пути со скоростью, меньшей скорости первого на 10 км/ч, а вторую половину пути – со скоростью 60 км/ч, в результате чего прибыл в пункт В одновременно с первым автомобилем.

Найдите скорость первого автомобиля, если известно, что она больше 39 км/ч. Ответ дайте в км/ч.

Решение:

+ показать

1. Так как автомобили выехали одновременнно из А и прибыли одновременно в В, то
2. Откуда или .
3. В условии задачи сказано, что скорость первого автомобиля больше 39 км/ч, поэтому оставляем только вариант
4. Ответ: 40.

Задание 5

Из двух городов, расстояние между которыми равно 300 км, навстречу друг другу одновременно выехали два автомобиля. Через сколько часов автомобили встретятся, если их скорости равны 70 км/ч и 80 км/ч?

• Решение:
• + показать
• Обозначим за ч время нахождения в пути одного автомобиля до встречи с другим.
• Тогда один из автомобилий прошел , второй – км.
• В сумме эти пути дают км.
• Поэтому
• Ответ: 2.

Задание 6

Из городов A и B, расстояние между которыми равно 300 км, навстречу друг другу одновременно выехали два автомобиля и встретились через 2 часа на расстоянии 160 км от города B. Найдите скорость автомобиля, выехавшего из города A. Ответ дайте в км/ч.

1. Решение:
2. + показать

Встреча произошла ближе к А. То есть автомобиль, выехавший из А, проехал меньший путь, нежели автомобиль из В.

Итак,  скорость движения автомобиля, выехавшего из А, есть км/ч.

Ответ: 70.

Задание 7.

Расстояние между городами A и B равно 620 км. Из города A в город B выехал первый автомобиль, а через два часа после этого навстречу ему из города B выехал со скоростью 90 км/ч второй автомобиль. Найдите скорость первого автомобиля, если автомобили встретились на расстоянии 350 км от города A. Ответ дайте в км/ч.

• Решение:
• + показать
• Второй автомобиль проехал км со скоростью км/ч, значит он находился в пути часа.
• Первый автомобиль находился в пути на два часа больше, то есть 5 часов.
• Поэтому скорость первого автомобиля, проехавшего км за 5 часов есть км/ч.
• Ответ: 70.

Задание 8.

Товарный поезд каждую минуту проезжает на 450 метров меньше, чем скорый, и на путь в 240 км тратит времени на 2 часа больше, чем скорый. Найдите скорость товарного поезда. Ответ дайте в км/ч.

1. Решение:
2. + показать
3. Прежде всего, переведем м/мин в км/ч.
4. м/мин=км/мин=км/ч=км/ч.

Обозначаем за км/ч скорость скорого поезда. Тогда скорость товарного – км/ч.

• Заполняем таблицу:
• («Страшные дискриминанты» мы обсуждали здесь)
• Откуда Тогда скорость товарного поезда км/ч.
• Ответ: 45.

Задание 9.

Расстояние между городами A и B равно 198 км. Из города A в город B выехал автомобиль, а через 3 часа следом за ним со скоростью 80 км/ч выехал мотоциклист, догнал автомобиль в городе C и повернул обратно. Когда он вернулся в A, автомобиль прибыл в B. Найдите расстояние от A до C. Ответ дайте в километрах.

Решение:

+ показать

Пусть расстояние от A до C – км. Так как скорость мотоциклиста км/ч, то время в пути AC мотоциклиста – . По условию сказано, что автомобиль в пути AC находился на 3 часа больше, поэтому указываем в таблице время нахождения автомобиля в пути AC – часов.

1. Далее, автомобиль проделывает путь CB, длина которого выражается у нас через , а мотоциклист возвращается обратно, то есть проделывает все тот же путь CA с той же скоростью  км/ч за тоже время .
2. Скорость автомобилиста на пути CB, также как и скорость на пути AC, есть или км/ч.
3. Поэтому расстояние с этой скоростью он пройдет за время часов.
4. Время прохождения автомобилистом пути CB равно времени прохождения пути CA мотоциклистом, поэтому
5. Вычисление корня квадратного из большого числа – смотрите здесь.
6. Откуда
7. Ответ: 144.

Задание 10.

Два пешехода отправляются одновременно в одном направлении из одного и того же места на прогулку по аллее парка. Скорость первого на 1,5 км/ч больше скорости второго. Через сколько минут расстояние между пешеходами станет равным 475 метрам?

• Решение:
• + показать
• Обозначаем за м/мин скорость второго пешехода и за м – пройденный им путь.
• Заметим, км/ч=м/мин.
• Ответ: 19.

Задание 11.

Первый велосипедист выехал из поселка по шоссе со скоростью 15 км/ч. Через час после него со скоростью 12 км/ч из того же поселка в том же направлении выехал второй велосипедист, а еще через час после этого  — третий. Найдите скорость третьего велосипедиста, если сначала он догнал второго, а через 2 часа 20 минут после этого догнал первого. Ответ дайте в км/ч.

1. Решение:
2. + показать
3. Обозначим за (км/ч) скорость третьего велосипедиста.

Обозначим за (ч) время, прошедшее от старта третьего велосипедиста до встречи  со вторым. За это время третий велосипедист проехал км.

• Тогда второй находился в пути до встречи с третьим велосипедистом часов и преодолел путь км.
• Имеем:
• Далее, первый велосипедист, согласно условию, находился в пути часов  до встречи второго и третьего велосипедистов и его путь за это время составил
• После этого первый, так же как и третий, проехали еще   по и км соответственно.
• Итак,
• Нам предстоит решить систему:
• Откуда получаем:
•  или
• Конечно же, второй вариант не подходит, так как скорость третьего велосипедиста явно должна быть больше 12 км/ч, иначе он никого не сможет перегнать.
• Ответ: 24.

Задание 12.

Поезд, двигаясь равномерно со скоростью 60 км/ч, проезжает мимо придорожного столба за 30 секунд. Найдите длину поезда в метрах.

1. Решение:
2. + показать
3. Согласно условию за 30 секунд поезд проходит расстояние, равное своей длине .
4. Чтобы найти длину поезда , нужно скорость поезда умножить на секунд.
5. При этом, заметьте, требуется перевод всех данных в один формат.
6. км/ч= м/с м/с.
7. Тогда (м).
8. Ответ: 500.

Задание 13.

Поезд, двигаясь равномерно со скоростью 80 км/ч, проезжает мимо лесополосы, длина которой равна 500 метров, за 36 секунд. Найдите длину поезда в метрах.

• Решение:
• + показать
• Согласно условию за 36 минут поезд проходит м, где – длина поезда.
• Переведем км/ч в м/мин:
• км/ч=м/мин=м/сек.
• Тогда
• (м).
• Ответ: 300.

Задание 14.

По двум параллельным железнодорожным путям в одном направлении следуют пассажирский и товарный поезда, скорости которых равны соответственно 80 км/ч и 50 км/ч. Длина товарного поезда равна 1200 метрам. Найдите длину пассажирского поезда, если время, за которое он прошел мимо товарного поезда, равно 3 минутам. Ответ дайте в метрах.

1. Решение:
2. + показать
3. Переведем сразу км/ч в м/мин:
4. км/ч=м/мин= м/мин.
5. км/ч=м/мин= м.
6. За 3 минуты товарный поезд прошел   м:
7. (м),
8. а пассажирский (м).
9. Согласно условию пассажирский поезд за 3 минуты прошел путь, равный м.
10. Тогда
11. м.
12. Ответ: 300.

Смотрите фрагмент видеолекции

Живы еще? 😉 =>+ показать

Побольше оптимизма! И все будет хорошо!

•  
  Вы можете пройти тест по задачам на движение по прямой.
• egeMax |

Чтобы не потерять страничку, вы можете сохранить ее у себя:

Печать страницы

Источник: https://egemaximum.ru/13-5/

Тест автомобилей на скорости в 200 км/ч, на что способны современные авто?

Для одних автомобилей 200 км/ч считается пределом, другие пролетят его мимоходом и даже не заметят. Давайте вместе посмотрим и убедимся, насколько приспособлены современные автомобили к передвижению со скоростью 200 км/ч. Удобно ли лететь быстрее стрижа в современном автомобиле, и какие всевозможные неудобства поджидают автомобилистов при этой скорости.

Раньше все было по-другому, а именно, чтобы разогнаться до скорости 200 км/ч – это было чем-то сверх необычным, словно преодолеваешь звуковой барьер! Мало каким из автомобилей это удавалось.

А кому в этом плане все же повезло заполучить подобный автомобиль, особого комфорта в нем не ощущали, только и знай, что следи постоянно за поведением авто на дороге, а то чего доброго можно и улететь с нее. Мда..

, в 90-е годы понервничать приходилось серьёзно и не мало, потные ладони на руле, сосредоточенный взгляд, постоянное чувство опасности. А сейчас также, или все изменилось? Давайте вместе разбираться.

Тестирование было проведено командой немецкого автомобильного журнала AutoBild.

200 км/ч не предел. Границы преодолены.

Сегодня конечно все по-другому. По крайней мере, если вопрос рассматривать с технической точки зрения. В настоящее время автомобили нового поколения, т.е. как минимум из Европы или Америки мощностью более 140 л.с. и с правильной аэродинамикой (седаны, кабриолеты, купе, универсалы) способны превзойти эту магическую цифру.

Несколько десятков секунд напряженного разгона и вот уже стрелка спидометра лежит за отметкой в 200 км/ч. Да что там 200 км, даже маленький хэтч Opel Corsa OPC сегодня может летать со скоростью 230 км/ч. Более того, даже автобусы типа VW T6 2.

0 TDI по паспорту обладают максималкой более чем в 203 км/ч, где шум завывающего за окном ветра никому не будет досаждать.

Но все эти показатели так и остаются на бумаге даже в том плане, что многие автомобили способны на излете сил преодолевать магический барьер, но… А что дальше? Смогут ли они долго двигаться в таком режиме не сводя с ума своих пассажиров? Ведь физику не изменишь и существуют аэродинамические ограничения. Сопротивление воздуха в конце-то концов увеличивается значительно и в разы.

А вот физиология самого человека не всегда способна выдержать такие гонки, тем-более если автомобиль не обладает достаточной или великолепной управляемостью. Факторов влияющих на комфорт водителя и пассажиров множество. Это, как мы уже выше сказали, то же сопротивление воздуха и возможности самой тормозной системы автомобиля, та же курсовая устойчивость и отзывчивость самого водителя.., и т.д.

и т.п.

Не стоит забывать конечно и о том, что летящий со скоростью 200 км/ч автомобиль за 1 секунду преодолевает расстояние в 55 метров. А это уже не шутки!

И так после всего сказанного расстановка сил ясна. Отсюда следует вывод, что не каждый водитель в том или ином автомобиле может справиться с поставленной задачей.

В этой истории нас интересует такая тема, -что происходит с автомобилями при скорости 200 км/ч. и на сколько может современная техника выдержать эту скорость? А также, -как чувствует себя водитель в тот самый момент? И последнее, что немаловажно, -сколько топлива сожжется при таких заездах?

В тестировании приняли участие десять автомобилей, от подержанного Mercedes-Benz модели C 180 с пробегом 420 тыс. км и вплоть до супер спортсмена, 580-ти сильного Porsche 911 Turbo S. Все они прошли замеры по уровню шума в салоне, потреблению топлива и по торможению со скорости.

Уровни измерений по всем автомобилям разнились. Для старичка Mercedes были сделаны некоторые поблажки, в упражнении на «торможение», для мощного американского пикапа Dodge Ram порог максимальной скорости был снижен до 195 км/ч (из соображений безопасности).

У Mercedes-Benz V-Class возникли сложности в разгоне до 200 км/ч на тестовом 2.6 километровом полигоне.

Дополнительные значения измерений: десять кандидатов должны были, как минимум, доказать возможность их ускорения в различных условиях.

Погрешность спидометра была определена при помощи GPS технологий, также немаловажную роль в исследовании играли обороты двигателя при данной скорости. Помимо динамики с 0 до 200 км/ч было замерено время разгона, т.е.

со 130 до 200 км/ч. Субъективно оценивалась шумность и прямолинейность движения.

• В испытаниях на скоростях участвовали:
• Abarth Spider
• Audi Q5
• BMW M550i
• Dodge Ram
• Lexus IS
• Mercedes C-Class
• Mercedes V-Class
• Porsche 911 Turbo
• VW Golf
• VW Passat

Abarth Spider

Легкий, компактный и маневренный. Abarth Spider создан для того, чтобы быть быстрым и удобным в управлении на больших скоростях.

Да конечно, мощности для преодоления рубежа в 200 км/ч ему хватает и еще на скорости для водителя возникают непредвиденные неудобства.

Шумоизоляция у Spider Abarth сделана из рук вон плохо. Слышны серьезные завывания ветра и тот же шум покрышек. Прибавляем ко всему этому звук работающего на повышенных оборотах двигателя (меньшее из зол) и в конечном итоге получаем -86 дБ. Это много. Это примерно сопоставимо с громким криком или работой мотоцикла с глушителем.

Несмотря на легкий кузов при скорости 200 км Abarth сжигает топлива 17,7 литра на 100 км. Показатель незаоблачный, но и не малый.

На шестой передаче коленвал 1.4 литрового турбированного бензинового двигателя вращается со скоростью около 5.100 оборотов в минуту. Субъективно можно предположить, что двигателю очень непросто выдерживать такой темп езды и причем надо заметить, что 200 км/ч на спидометре это фактические 193 км/ч по GPS.

Audi Q5

 Передние двойные оконные стекла (многослойное стекло доступно за доп. плату в размере 150 евро) позволяют снизить уровень шума на скорости. Четырехцилиндровый двигатель 2.

0 TFSI под капотом Audi Q5 неплохо изолирован и пробивается в салон незначительным звуковым сопровождением.

Даже на скорости 200 км/ч проблем с досаждающими звуками на этом кроссовере не было, как и по аэродинамическим показателям.

Источник: http://www.1gai.ru/test-drayvy/519182-test-avtomobiley-na-skorosti-v-200-km-ch-na-chto-sposobny-sovremennye-avto.html

Движение навстречу друг другу

Задачи на движение навстречу друг другу (встречное движение) — один из трех основных видов задач на движение.

Если два объекта движутся навстречу друг другу, то они сближаются:

• Чтобы найти скорость сближения двух объектов, движущихся навстречу друг другу, надо сложить их скорости:  
• Скорость сближения больше, чем скорость каждого из них.
• Скорость, время и расстояние связаны между собой формулой пути:
• Рассмотрим некоторые задачи на встречное движение.
• Задача 1

Два велосипедиста выехали навстречу друг другу. Скорость одного из низ 12 км/ч, а другого — 10 км/ч. Через 3 часа они встретились. Какое расстояние было между ними в начале пути?

Решение:

Условие задач на движение удобно оформлять в виде таблицы:

v, км/ч	t, ч	s, км
I велосипедист	12	3	?
II велосипедист	10	3	?

1. 1) 12+10=22 (км/ч) скорость сближения велосипедистов
2. 2) 22∙3=66 (км) было между велосипедистами в начале пути.
3. Ответ: 66 км.
4. Задача 2

Два поезда идут навстречу друг другу. Скорость одного из них 50 км/ч, скорость другого —  60 км/ч. Сейчас между ними 440 км. Через сколько часов они встретятся?

Решение:

v, км/ч	t, ч	s, км
I поезд	60	?	?
II поезд	50	?	?

• 1) 60+50=110 (км/ч) скорость сближения поездов
• 2) 440:110=4 (ч) время, через которое поезда встретятся.
• Ответ: через 4 ч.
• Задача 3.

Два пешехода находились на расстоянии 20 км друг от друга. Они вышли одновременно навстречу друг другу и встретились через 2 часа. Скорость одного пешехода 6 км/ч. Найти скорость другого пешехода.

v, км/ч	t, ч	s, км
I пешеход	6	2	?
II пешеход	?	2	?

1. 1) 20:2=10 (км/ч) скорость сближения пешеходов
2. 2) 10-6=4 (км/ч) скорость другого пешехода.
3. Ответ: 4 км/ч.

Источник: http://www.for6cl.uznateshe.ru/dvizhenie-navstrechu-drug-drugu/

Блог учителя математики Крымовой Е.В

•  ( №1 – №7 
  5 – 6 класс, №8 дробно – рациональное)
• Вариант  00
• №1  Задание B14 (№ 112399)    

Из двух городов, расстояние между которыми равно 480
км, навстречу друг другу одновременно выехали два автомобиля. Через сколько
часов автомобили встретятся, если их скорости равны 75 км/ч и 85 км/ч?

1.                              480 км
2. Решение:
3. 1)   75 + 85 = 160 ( км/ч) – скорость сближения
4. 2)   480 : 160 = 3 ( ч) – автомобили встретятся
5. Ответ: 3
6.   №2  Задание B14 (№ 112459)    

Из городов A и B, расстояние между которыми равно 440
км, навстречу друг другу одновременно выехали два автомобиля и встретились
через 4 часа на расстоянии 240 км от города B. Найдите скорость автомобиля,
выехавшего из города A. Ответ дайте в км/ч.

• Решение:
• 1    1)     440 – 240 = 200 ( км) –
  расстояние, которое проехал автомобиль выехавший из города A
•        2)      200 : 4 = 50 (км/ч) скорость автомобиля выехавшего из города A
• Ответ: 50
• № 3   Задание B14 (№ 112519)

Расстояние между городами A и B равно 440 км. Из города A в город B со
скоростью 50 км/ч выехал первый автомобиль, а через час после этого навстречу
ему из города B выехал со скоростью 80 км/ч второй автомобиль. На каком
расстоянии от города A автомобили встретятся? Ответ дайте в километрах.

1. Решение:
2. 1)      440 – 50 = 390 ( км ) расстояние между автомобилями в момент начала движения второго автомобиля
   ( выехавшего из пункта В)
3. 2)      50 + 80 = 130 ( км/ч)
   скорость сближения
4. 3)      390 : 130 = 3 (ч)
   время движения второго автомобиля
5. 4)      3 + 1 = 4 ( ч) время
   движения  первого автомобиля
6. 5)     
   50 · 4 = 200( км) расстоянии от города
   A на котором автомобили встретятся
7. Ответ: 200
8. №4  Задание B14 (№ 112803)    

Расстояние между городами A и B равно 680 км. Из
города A в город B выехал первый автомобиль, а через два часа после этого
навстречу ему из города B выехал со скоростью 80 км/ч второй автомобиль.
Найдите скорость первого автомобиля, если автомобили встретились на расстоянии
360 км от города A. Ответ дайте в км/ч.

• Решение:
• 1)       680 – 360 = 320
  ( км ) ( расстояние  пройденное
  автомобилем, выехавшим  из пункта В)
• 2)      320 : 80 = 4 (ч)
  время движения второго автомобиля
• 3)       4 + 2 = 6 ( ч) время движения  первого автомобиля
• 4)      360 : 6 = 60 ( км/ч)
  скорость первого автомобиля
• Ответ: 60

Источник: http://matematichka75.blogspot.com/2014/04/14-1-1-7-6-8-00-1-b14-112399-480.html

Учимся решать задачи на движение – Диагностическая работа

Д1. Из двух городов, расстояние между
которыми равно 560 км, навстречу друг другу одновременно выехали два
автомобиля. Через сколько часов автомобили встретятся, если их скорости равны
65 км/ч и 75 км/ч?

Ответ: 4.

Д2. Из посёлка A в посёлок В, расстояние
между которыми равно 30 км, выехал грузовик, а через 6 минут следом за ним
выехал автобус, скорость которого на 10 км/ч больше скорости грузовика. Найдите
скорость автобуса, если в посёлок В он прибыл одновременно с грузовиком. Ответ
дайте в км/ч.

Ответ: 60.

Д3. Два мотоциклиста стартуют
одновременно в одном направлении из двух диаметрально противоположных точек
круговой трассы, длина которой равна 14 км. Через сколько минут мотоциклисты
поравняются в первый раз, если скорость одного из них на 21 км/ч больше
скорости другого?

Ответ: 20.

Д4. Половину времени, затраченного на
дорогу, автомобиль ехал со скоростью 74 км/ч, а вторую половину времени — со скоростью
66 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ
дайте в км/ч.

Ответ: 70.

 Д5. Поезд, двигаясь равномерно со
скоростью 80 км/ч, проезжает мимо придорожного столба за 36 секунд. Найдите
длину поезда в метрах.

Ответ: 800.

Д6. Из городов А и В, расстояние между
которыми равно 330 км, навстречу друг другу одновременно выехали два автомобиля
и встретились через 3 часа на расстоянии 180 км от города B. Найдите скорость
автомобиля, выехавшего из города A. Ответ дайте в км/ч.

Ответ: 50.

 Д7. Путешественник переплыл море на яхте
со средней скоростью 20 км/ч. Обратно он летел на спортивном самолете со
скоростью 480 км/ч. Найдите среднюю скорость путешественника на протяжении
всего пути. Ответ дайте в км/ч.

Ответ: 38,4.

 Д8. Поезд, двигаясь равномерно со
скоростью 60 км/ч, проезжает мимо лесополосы, длина которой равна 400 метрам,
за 1 минуту. Найдите длину поезда в метрах.

Ответ: 600.

 Д9. Расстояние между городами A и B равно
470 км. Из города A в город B выехал первый автомобиль, а через 3 часа после
этого навстречу ему из города B выехал со скоростью 60 км/ч второй автомобиль.
Найдите скорость первого автомобиля, если автомобили встретились на расстоянии
350 км от города A. Ответ дайте в км/ч.

Ответ: 70.

Д10. Часы со стрелками показывают 8 часов
00 минут. Через сколько минут минутная стрелка в четвертый раз поравняется с
часовой?

Ответ: 240.

Д11. Первые два часа автомобиль ехал со
скоростью 50 км/ч, следующий час — со скоростью 100 км/ч, а последние два часа —
со скоростью 75 км/ч. Найдите среднюю скорость автомобиля на протяжении всего
пути. Ответ дайте в км/ч.

Ответ: 70.

 Д12. По двум параллельным железнодорожным
путям в одном направлении следуют пассажирский и товарный поезда, скорости
которых равны соответственно 90 км/ч и 30 км/ч. Длина товарного поезда равна
600 метрам. Найдите длину пассажирского поезда, если время, за которое он
прошел мимо товарного поезда, равно 1 минуте. Ответ дайте в метрах.

Ответ: 1400.

Д13. Товарный поезд каждую минуту
проезжает на 750 метров меньше, чем скорый, и на путь в 180 км тратит времени на
2 часа больше, чем скорый. Найдите скорость товарного поезда. Ответ дайте в
км/ч.

Ответ: 45.

Д14. Первые 100 км автомобиль ехал со
скоростью 100 км/ч, следующие 200 км — со скоростью 50 км/ч, а последние 300 км
— со скоростью 60 км/ч. Найдите среднюю скорость автомобиля на протяжении всего
пути. Ответ дайте в км/ч.

Ответ: 60.

Д15. По двум параллельным железнодорожным
путям друг навстречу другу следуют скорый и пассажирский поезда, скорости которых
равны соответственно 65 км/ч и 35 км/ч. Длина пассажирского поезда равна 700
метрам. Найдите длину скорого поезда, если время, за которое он прошел мимо
товарного поезда, равно 36 секундам. Ответ дайте в метрах.

Ответ: 300.

Таблица с ответами

Задание	Д1	Д2	Д3	Д4	Д5	Д6	Д7	Д8	Д9	Д10	Д11	Д12	Д13	Д14	Д15
Ответ	4	60	20	70	800	50	38,4	600	70	240	70	1400	45	60	300

Источник: https://matematika-2013.ucoz.com/index/diagnosticheskaja_rabota/0-11

Задачи на движение (нахождение скорости) с ответами

Из поселка и города навстречу друг другу, одновременно выехали два автобуса. Один автобус до встречи проехал 100 км со скоростью 25 км/час. Сколько километров до встречи проехал второй автобус, если его скорость 50 км/час.

Решение:

• 1) 100 : 25 = 4 (часа ехал один автобус)
• 2) 50 * 4 = 200
• Выражение: 50 * (100 : 25) = 200
• Ответ: второй автобус проехал до встречи 200 км.

Задача 2

Расстояние между двумя пристанями 90 км. От каждой из них одновременно навстречу друг другу вышли два теплохода. Сколько часов им понадобится чтобы встретиться, если скорость первого 20 км/час, а второго 25 км/час?

Решение:

• 1) 25 + 20 = 45 (сумма скоростей теплоходов)
• 2) 90 : 45 = 2
• Выражение: 90 : (20 + 25) = 2
• Ответ: теплоходы встретятся через 2 часа.

Задача 3

От двух станций, расстояние между которыми 564 км., одновременно навстречу друг другу вышли два поезда. Скорость одного из них 63 км/час. Какова скорость второго, если поезда встретились через 4 часа?

Решение:

• 1) 63 * 4 = 252 (прошел 1 поезд)
• 2) 564 – 252 =312 (прошел 2 поезд)
• 3) 312 : 4 = 78
• Выражение: (63 * 4 – 252) : 4 = 78
• Ответ: скорость второго поезда 78 км/час.

Задача 4

Через сколько секунд встретятся две ласточки, летящие на встречу друг другу, если скорость каждой из них 23 метра в секунду, а расстояние между ними 920 м.

Решение:

• 1) 23 * 2 = 46 (сумма скоростей ласточек)
• 2) 920 : 46 = 20
• Выражение: 920 : (23 * 2) = 20
• Ответ: ласточки встретятся через 20 секунд.

Задача 5

С двух поселков, навстречу друг другу выехали одновременно велосипедист и мотоциклист. Скорость мотоциклиста 54 км/час, велосипедиста 16 км/час. Сколько километров проехал мотоциклист до встречи, если велосипедист проехал 48 км?

Решение:

• 1) 48 : 16 = 3 (часа потратил велосипедист)
• 2) 54 * 3 = 162
• Выражение: 54 * (48 : 16) = 162
• Ответ: мотоциклист проехал 162 км.

Задача 6

Две лодки, расстояние между которыми 90 км, начали движение на встречу друг другу. Скорость одной из лодок 10 км /час, другой 8 км/час. Сколько часов понадобится лодкам, чтобы встретится?

Решение:

• 1) 10 + 8 = 18 (скорость двух лодок вместе)
• 2) 90 : 18 = 5
• Выражение: 90 : (10 + 8) = 5
• Ответ: лодки встретятся через 5 часов.

Задача 7

По дорожке, длинна которой 200 метров, навстречу друг другу побежали два мальчика. Один из них бежал со скоростью 5 м/сек. Какова скорость второго мальчика, если встретились они через 20 сек?

Решение:

• 1) 20 * 5 = 100 (метров пробежал первый мальчик)
• 2) 200 – 100 = 100 (метров пробежал второй мальчик)
• 3) 100 : 20 = 5
• Выражение: (200 – 5 * 20) : 20 = 5
• Ответ: скорость второго мальчика 5 км/сек.

Задача 8

Два поезда выехали навстречу друг другу. Скорость одного из них 35 км/час, другого 29 км/час. Какое расстояние между поездами было сначала, если встретились они через 5 часов?

Решение:

• 1) 35 + 29 = 64 (скорсть двух поездов вместе)
• 2) 64 * 5 = 320
• Выражение: (35 + 29) * 5 = 320
• Ответ: расстояние между поездами было 320 км.

Задача 9

Из двух поселков навстречу друг другу выехали два всадника. Скорость одного из них 13 км/час, встретились они через 4 часа. С какой скоростью двигался второй всадник, если расстояние между поселками 100 км.

Решение:

• 1) 13 * 4 = 52 (проехал первый всадник)
• 2) 100 – 52 = 48 (проехал второй всадник)
• 3) 48 : 4 = 12
• Выражение: (100 – 13 * 4) : 4 = 12
• Ответ: скорость второго всадника 12 км/час.

Задача 1

Грузовой поезд проехал 420 км, сделав остановку на одной станции. Путь до этой станции занял 4 часа при скорости 80км/час. Весь оставшийся путь занял 2 часа. С какой скоростью поезд двигался после остановки?

Решение:

• 1) 4 * 80 = 320
• 2) 420 – 320 = 100
• 3) 100 : 2 = 50
• Ответ: Поезд после остановки двигался со скоростью 50 км/час

Задача 2

Грузовик в первый день проехал 600 км, а во второй день 200 км. Весь путь занял 8 часов. Сколько часов в день проезжал грузовик, если он ехал все время с одинаковой скоростью.

Решение:

• 1) 600 + 200 = 800
• 2) 800 : 8 = 100
• 3) 600 : 100 = 6
• 4) 200 : 100 = 2
• Ответ: в первый день 6 часов, во второй 2 часа.

Задача 3

Велосипедист проезжает путь из города в поселок, со скоростью 17 км/час, за 5 часов. Сколько времени потребуется пешеходу, что бы пройти этот же путь, если он движется со скоростью 5 км/час?

Решение:

• 1) 17 * 5 = 85
• 2) 85 : 5 = 17
• Ответ: пешеходу понадобится 17 часов.

Задача 4

Автомобиль проехал 400 километров. Двигаясь со скоростью 60 км/час, он проехал за 2 часа первую часть пути. С какой скоростью он двигался остальную часть пути, если он затратил на нее 4 часа?

Решение:

• 1) 60 * 2 = 120
• 2) 400 – 120 = 280
• 2) 280 : 4 = 70
• Ответ: 70 км/час

Задача 5

Скворец летел со скоростью 75 км/час 2 часа. С какой скоростью летит ворона, если такое же расстояние она пролетит за 3 часа?

Решение:

• 1) 75 * 2 = 150
• 2) 150 : 3 = 50
• Ответ: скорость вороны 50 км/час.

Задача 6

Автотуристы были в пути 15 часов в течение 2 дней. 420 километров они проехали в первый день и 480 во второй. Сколько часов каждый день они были в пути, если каждый день они двигались с одинаковой скоростью?

Решение:

• 1) 420 + 480 = 900
• 2) 900 : 15 = 60
• 3) 420 : 60 = 7
• 4) 480 : 60 = 8
• Ответ: в первый день 7 часов, во второй 8.

Задача 7

От города до поселка 37 километров, а от этого поселка до следующего 83 км. Сколько времени понадобиться, что бы доехать от города до последнего поселка, если двигаться со скоростью 40 км/час?

Решение:

• 1) 37 + 83 = 120
• 2) 120 : 4 = 3
• Ответ: 3 часа.

Задача 8

За 3 часа катер преодолел расстояние в 210 км. Какое расстояние оно пройдет за 5 часов, если его скорость увеличится на 5 км/час?

Решение:

• 1) 210 : 3 = 70
• 2) 70 + 5 = 75
• 3) 75 * 5 = 375
• Ответ: 375 км.

Задача 9

Теплоход за 9 часов прошел 360 км в первый день. Во второй день теплоход с прежней скоростью был в пути 12 часов. Сколько всего километров преодолел теплоход за 2 дня?

Решение:

• 1) 360 : 9 = 40
• 2) 40 * 12 = 480=
• 3) 480 + 360 = 840
• Ответ: 840 км.

Задача 10

Вертолет пролетает за 4 часа 960 километров. Сколько времени понадобится самолету, чтобы пролететь то же расстояние, если он движется в 2 раз быстрее?

Решение:

• 1) 960 : 4 = 240
• 2) 240 * 2 = 480
• 3) 960 : 480 = 2
• Ответ: 2 часа

Задача 1

Машина и автобус выехали с автостанции одновременно в противоположных направлениях. Скорость автобуса в два раза меньше скорости автомобиля. Через сколько часов расстояние между ними будет 450 км, если скорость автомобиля 60 км/час?

Решение:

• 1) 60 : 2 = 30 (скорость автобуса)
• 2) 60 + 30 = 90 (скорость автобуса и автомобиля вместе)
• 3) 450 : 90 = 5
• Выражение: 450 : (60 : 2 + 60) = 5
• Ответ: через 5 часов.

Задача 2

Из города на дачу выехал велосипедист со скоростью 12 км/час. Дорога на дачу заняла 6 часов. На сколько изменилась скорость велосипедиста на обратном пути, если он затратил на него 4 часа?

Решение:

• 1) 12 * 6 = 72 (расстояние от города к даче)
• 2) 72 : 4 = 18 (скорость обратного пути велосипедиста)
• 3) 18 – 12 = 6
• Выражение: (12 * 6 : 4) – 12 = 6
• Ответ: скорость велосипедиста увеличилась на 6 км/час.

Задача 3

Два поезда одновременно начали движение в противоположных на правлениях. Один двигался со скоростью на 30 км/час меньше, чем другой. На каком расстоянии друг от друга поезда будут через 4 часа, если скорость другого поезда 130 км/час?

Решение:

• 1) 130 – 30 = 100 (км/час скорсть второго поезда)
• 2) 130 + 100 = 230 (скорость двух поездов вместе)
• 3) 230 * 4 = 920
• Выражение: (130 – 30 + 130) * 4 = 920
• Ответ: расстояние между поездами через 4 часа будет 920 км.

Задача 4

Такси двигалось со скоростью 60 км/час, автобус в 2 раза медленнее. Через сколько времени между ними будет 360 км, если они движутся в разных направлениях?

Решение:

• 1) 60 : 2 = 30 (скорость автобуса)
• 2) 60 + 30 = 90 (скорость автобуса и такси вместе)
• 3) 360 : 90 = 4
• Выражение: 360 : (60 : 2 + 60) = 4
• Ответ: через 4 часа.

Задача 5

Два автомобиля выехали из автопарка одновременно в противоположных направлениях. Скорость одного 70 км/час, другого 50 км/час. Какое расстояние будет между ними через 4 часа?

Решение:

• 1) 70 + 50 = 120 (скорость двух автомобилей вместе)
• 2) 120 * 4 = 480
• Выражение: (70 + 50) : 4 = 480
• Ответ: через 4 часа между автомобилями будет 480 км.

Задача 6

Два человека в одно и тоже время вышли из поселка в разных направлениях. Один двигался со скоростью 6 км/час, скорость другого была 5 км/час. Сколько часов понадобится чтобы расстояние между ними стало 33 км?

Решение:

• 1) 6 + 5 = 11 (скорость двух человек вместе)
• 2) 33 : 11 = 3
• Выражение: 33 : ( 6 + 5) = 3
• Ответ: через 3 часа.

Задача 7

Грузовой и легковой автомобили отправились от автостанции в разных направлениях. За одно и тоже время грузовик проехал 70 км, а легковой автомобиль 140 км. С какой скоростью двигался легковой автомобиль, если скорость грузовика 35 км/час?

Решение:

• 1) 70 : 35 = 2 (часа затратил на дорогу грузовик)
• 2) 140 : 2 = 70
• Выражение: 140 : (70 : 35) = 70
• Ответ: скорость легкового автомобиля 70 км/час.

Задача 8

Два пешехода вышли из турбазы в противоположных направлениях. Скорость одного из них 4 км/час, другого 5 км/час. Какое расстояние будет между пешеходами через 5 часов?

Решение:

• 1) 4 + 5 = 11 (общая скорсть пешеходов)
• 2) 5 * 11 = 55
• Выражение: (4 + 5) * 5 = 55
• Ответ: через 5 часов между пешеходами будет 55 км.

Задача 9

Два самолета одновременно вылетели в противоположных направлениях. Скорость одного из самолетов 640 км/час. Какая скорость другого самолета, если через 3 часа расстояние между ними было 3630 км?

Решение:

• 1) 640 * 3 = 1920 (км пролетел один самолет)
• 2) 3630 – 1920 = 1710 (км пролетел другой самолет)
• 3) 1710 : 3 = 570
• Выражение: (3630 – 640 * 3) : 3 = 570
• Ответ: скорсть второго самолета 570 км/ч

Задача 10

Два крестьянина вышли из одного поселка одновременно в противоположных направлениях. Один двигался со скоростью 3 км/час другой 6 км/час. Какое расстояние будет между крестьянами через 5 часов.

Решение:

• 1) 3 + 6 = 9 (скорость двух крестьян вместе)
• 2) 5 * 9 = 45
• Выражение: 5 * (3 + 6) = 45
• Ответ: через 5 часов между крестьянами будет 45 км.

Источник: https://infourok.ru/zadachi-na-dvizhenie-nahozhdenie-skorosti-s-otvetami-728748.html